SAT考试里最难的数学题？

09 Sep 2015

问题

今天无意中在Quora上看到有人贴出来一道号称是SAT里最难的一道数学题，一下子勾起了我的兴趣。于是拿起笔来写写画画，花了差不多十五分钟搞定。觉得有点意思，决定把解题过程记下来。原帖的图太小，我用GeoGebra重新画了一遍。没错，我就是强迫症。

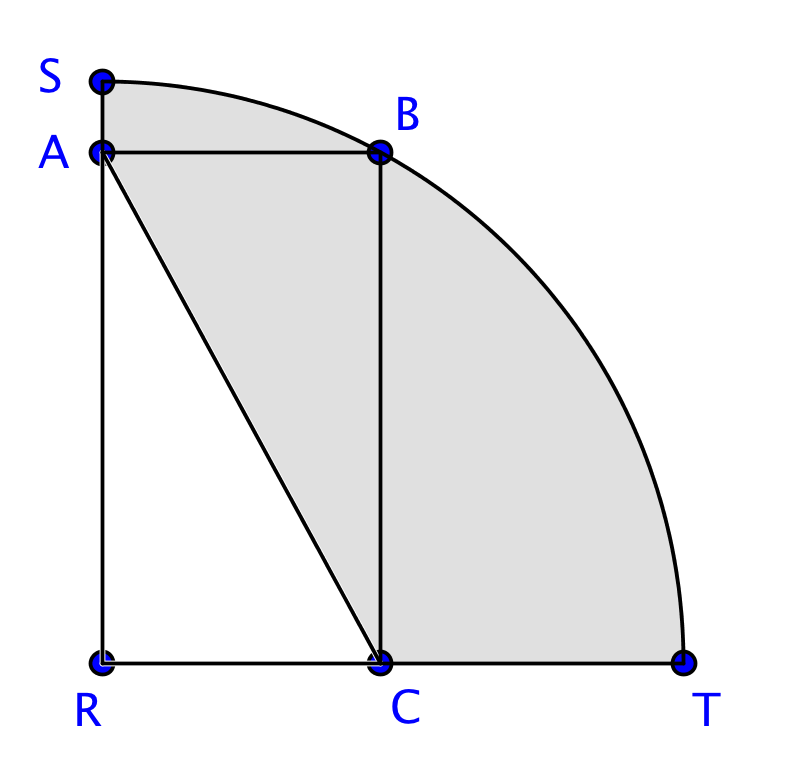
In the figure above, arc \(\text{SBT}\) is one quarter of a circle with center \(\text{R}\) and radius 6. If the length plus the width of rectangle \(\text{ABCR}\) is 8, then the perimeter of the shaded region is

翻译：上图中，弧\(\text{SBT}\)为四分之一圆；该圆圆心为\(\text{R}\)点，半径为6。若矩形\(\text{ABCR}\)的长、宽之和为8，则阴影部分的周长应为

1. \(8+3 \pi\)
2. \(10+3\pi\)
3. \(14+3\pi\)
4. \(1+6\pi\)
5. \(12+6\pi\)

解

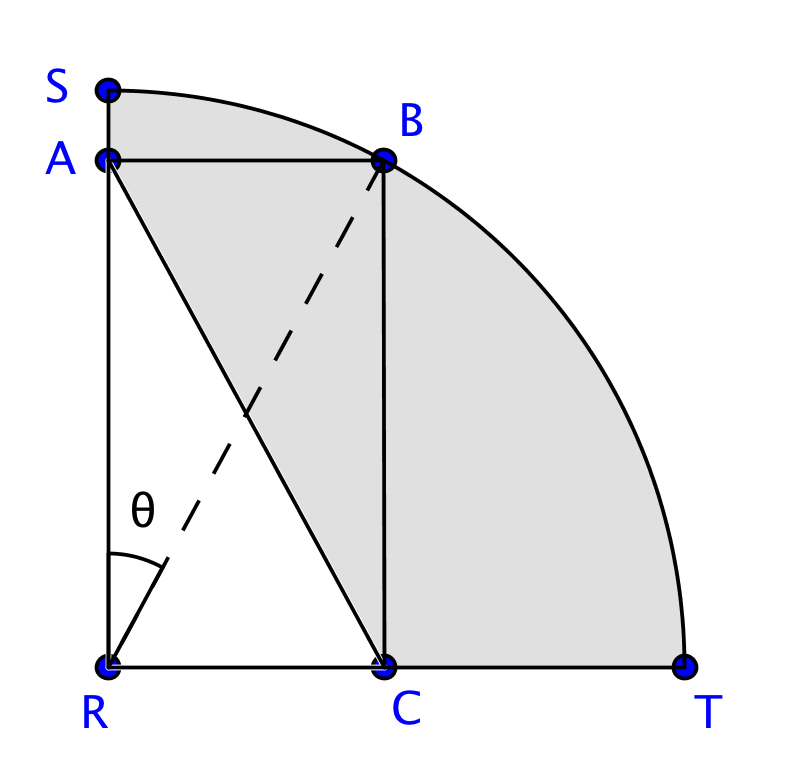
半径为6，即\( \text{SR}=\text{RT}=6 \)。如图作辅助线\(\text{RB}\)，设\(\theta=\angle{\text{ARB}}\)。

阴影区域周长\(L=\text{SA}+\text{AC}+\text{CT}+\widehat{\text{SBT}}\)。\(\widehat{\text{SBT}}\)是四分之一圆，所以

$$\widehat{\text{SBT}}=\frac{1}{4}\cdot 2\pi\cdot 6=3\pi$$

又因\(\text{ABCR}\)为矩形，得出\(\text{AC}=\text{RB}=6\)。因为圆弧的长为\(3\pi\)，排除两个圆弧部分是\(6\pi\)的答案；又因为剩余未知的

$$\begin{aligned} \text{SA}+\text{CT} &= \text{SR}+\text{RT} \\ &= 12-8 \\ &= 4 \\ \end{aligned}$$

所以选B，\(L=10+3\pi\)。

这……貌似没多难嘛，我高中毕业之后就没再碰过欧氏几何都没怎么费力气……¹

$$\square$$

没费力气才怪

如果只是上面几行字，怎么可能用上15分钟才解出来？上面的解法是我写这篇文章的时候才想到的；我下午花了十五分钟的解法，其实离走火入魔就差那么一点点。有没有注意到上面的解里根本没用上\(\theta\)？没错，\(\theta\)就是下午那会儿脑筋转不开的时候的产物。来看看我是如何绕圈解决\(\text{SA}+\text{CT}\)的吧：

要知道\(\text{SA}\)和\(\text{CT}\)，就要知道\(\text{AR}\)和\(\text{RC}\)。\(\text{AR}=\text{RB}\cos{\theta}=6\cos{\theta}\)，\(\text{AB}=\text{RB}\sin{\theta}=6\sin{\theta}\)。又有\(\text{AR}+\text{RC}=6\cos{\theta}+6\sin{\theta}=8\)，那么

$$\begin{aligned} \text{SA}+\text{CT} &= (6-6\cos{\theta})+(6-6\sin{\theta}) \\ &= 12-6(\cos{\theta}+\sin{\theta}) \\ &= 12-8 \\ &= 4 \end{aligned}$$

之所以用到三角函数，就是因为当时只想着暴力解出\(\text{AR}\)和\(\text{RC}\)来。我甚至已经解出了\(\sin{2\theta}=\frac{7}{9}\)来，差点就要反求\(\theta\)的值了……还好我适时地反问了一下自己：美国人的高中考试会有求反三角函数值的问题吗？选择题都要用科学计算器才能解出来的，那TMD是奥数²。

以上。